Policy Gradient笔记

思从何来

我尝试理解RLHF（Reinforcement Learning with Human Feedback），意识到我认知中的Q-Learning与当前RL有很大的出入，于是我学习了一下一些Deep Q-Learning的知识，记录一下学习的过程。

我认知中的RL

RL最通俗而最通用的解释就是这么一个模型：

1. 整个系统中有Agent、Envronment两个部分
2. 通过观测Environment得到状态$s_t$
3. Agent根据$s_t$选择最合适的动作$a_t$
4. 动作$a_t$作用于Environment，得到奖励$r_{t+1}$和新的状态$s_{t+1}$
5. Agent根据$r_{t+1}$和$s_{t+1}$更新自己的策略
6. 重复2-5步骤直至结束

对于每一个结局，我们都可以得到一个回报$R=\sum_{t=0}^{\infty}\gamma^t r_t$，其中$\gamma$是折扣因子(discount factor)，用于衡量未来奖励的重要性。
而整个强化学习的目标就是找到一个策略$\pi$，使得期望回报最大。

$$\pi^* = \arg\max_{\pi}E[R|\pi]$$

Tabular Q-Learning

从当前的状态$s$出发，我们如何选择最优的动作$a$，使得未来的回报最大呢？最容易想到的是贪心算法，即每一步都选择能够获得最大回报的动作。

贪心算法的问题在于，我们可能会陷入局部最优，而无法找到全局最优。为了解决这个问题，我们需要衡量每一个动作的价值，这个价值是一个综合考虑了当前动作的回报和未来动作的价值的一个值，那么我们就可以在每一步选择价值最大的动作，而不是直接选择回报最大的动作。

所以我们定义一个Q值，表示在状态$s$下，选择动作$a$的价值，即$Q(s,a)$。假设action space和state space都是有限的，那么我们可以用一个表格来存储Q值，表第$s$行第$a$列的值就是$Q(s,a)$，表示在状态$s$下选择动作$a$的价值。

有了这么一张表，我们只需要在每一个状态下选择最大的Q值对应的动作，就能得到一个全局最优策略。注意，这里指的是全局最优，而不是局部最优，因为我们的Q值是全局的，而不是局部的。获得这样一张表的方法就是Q-Learning，即学习每一个$(s,a)$对的Q值，使得最终的Q值表能够收敛到全局最优。

Q-Learning的更新公式如下：

$$Q^{k+1}(s_t,a_t) = Q^k(s_t,a_t) + \alpha(r_{t+1}+\gamma\max_{a}Q^k(s_{t+1},a)-Q^k(s_t,a_t))$$

其中$\alpha$是学习率，用于控制每次更新的幅度，$Q^k$表示第$k$次迭代的Q值表。可以这样理解这个更新公式：$Q^{k+1}$是$Q^k$的一个修正，修正的幅度由$r_{t+1}+\gamma\max_{a}Q^k(s_{t+1},a)-Q^k(s_t,a_t)$决定。

更新的增量的几个项分别表示：

1. $r_{t+1}$表示当前状态$s_t$选择动作$a_t$后得到的奖励
2. $\gamma$乘的这一项表示在下一个状态$s_{t+1}$下选择最优动作的Q值。也就是对$s_t$选择$a_t$后，接下来的最优策略的价值的一个估计
3. $Q^k(s_t,a_t)$表示当前状态$s_t$选择动作$a_t$的Q值，也就是当前策略的价值
4. 2-3项的差值表示当前策略和最优策略的差距，代表走这个动作能够获得的额外价值

与Superveised Learning不同，RL的目标是最大化回报，而不是最小化损失。此外RL的训练可以理解为遍历整个状态空间，而不是遍历整个数据集。这也是为什么RL的训练速度会比SL慢的原因。它停止的条件是策略收敛，也就是$|Q^{k+1} - Q^k| = \epsilon$，当$\epsilon$足够小时，我们就可以认为Q值表已经收敛。但是RL并不能保证收敛，因为Q值表的更新是基于贪心策略的，而贪心策略可能会陷入局部最优。
这一优化过程可以等价于最小化增量的平方和：

$$\min_{Q} \sum_{t=0}^{\infty}(Q^{k+1}(s_t,a_t) - Q^k(s_t,a_t))^2$$

这就是我认知中的Q-Learning，但是这个Q-Learning有一个很大的问题，那就是它只能处理离散的动作空间，而不能处理连续的动作空间。而且，它最优化的终点并不是Q值表保证每个$(s,a)$对的Q值都能代表最优策略，而是Q值表的收敛。

Deep Q-Learning

刚刚提到的TQL，有很大的局限性，那就是只能处理离散的动作空间。而这一问题的根源在于TQL的核心是Q table，而Q table是一个离散的表格，所以只能处理离散的动作空间。那如何能对连续空间的$(s,a)$对进行Q值的估计呢？这就是DQL的出发点。

Parametrize Q function

DQL的核心思想是，用一个函数来估计Q值，而不是用一个表格。我们用$\theta$来表示这个函数的参数，那么对于任意的$(s,a)$对，我们可以用$Q(s,a;\theta) \equiv Q_{\theta}(s,a)$来计算Q值。

DQN（Deep Q-learning Network）

假设有这样一款游戏，你的Agent需要操控右边的板子，选择向上还是向下移动，使得板子可以接住小球，而左边的板子是你的对手，你的目标是尽可能多的接住小球。这个游戏的状态空间是非常大，因为两块板子和小球的位置都是连续的，而动作空间是离散的，因为只有向上和向下两个动作。

对于这么大的状态空间而言，学习这样的一个Q table是不现实的。我们可以设计这么一个网络来计算Q值，从而选择向上还是向下。我们把状态建模成这么几个特征：

1. 小球的位置$x_{ball}$ $y_{ball}$
2. 对手板子的位置$y_{opponent}$
3. 你的板子的位置$y_{agent}$
4. 小球的速度$v^x_{ball}$ $v^y_{ball}$

简单设计这样一个网络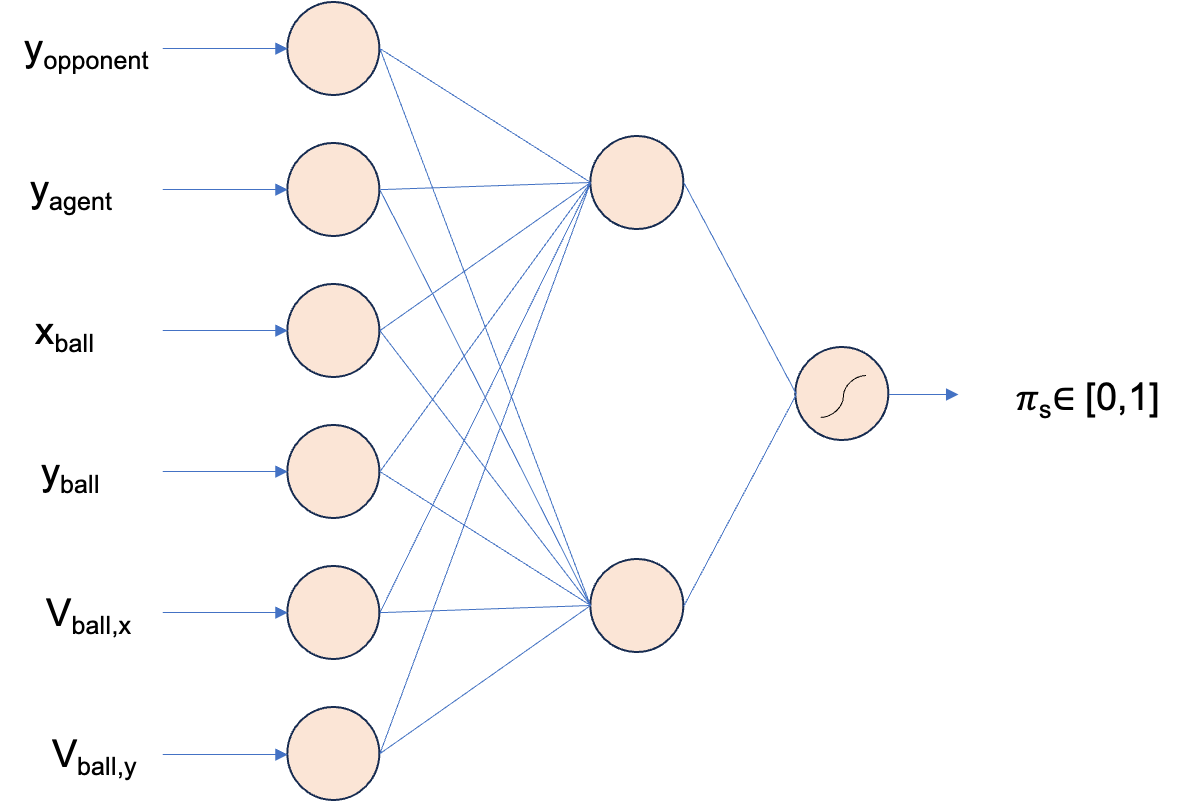

这个Q函数得到的结果是一个0-1之间的sigmoid值，表示向上（或者向下，这里只有两个动作，所以是相对的）的概率。通过优化这个网络的参数$\theta$，我们就可以得到一个最优的Q函数，使得在任意的状态下，选择最大的Q值对应的动作，就能得到一个全局最优的策略。有了这个网络，接下来要讨论的是，如何训练这个网络。

Policy Gradient

优化这个$\theta$ function的核心依然是，使得这个$\theta$ function的期望回报最大，这里就提到了两个东西：

1. 回报
2. 期望

回报很容易理解，我们做如下定义，从状态$s_0$开始，经过一系列的动作$a_0,a_1,...,a_n$游戏结束，对每一步$a_i$，我们都会得到一个奖励$r_i$，将agent与环境交互的这一整个过程称为一条轨迹(trajectory)，用符号$\tau$表示轨迹。那么这一条轨迹的回报就是

$$R(\tau) = \sum_{t=0}^{n}\gamma^t r_t$$

其中$\gamma$是折扣因子，是一个超参数，用于衡量未来奖励的重要性。而参数$\theta$的期望回报可以用经验分布的期望来计算，使用$\theta$的策略$\pi_{\theta}$采样一系列的轨迹，然后计算这些轨迹的回报的期望值，即

$$E[R(\tau)] = \sum_{\tau}P_{\theta}(\tau)R(\tau)$$

其中$P(\tau)$是轨迹的概率分布，是从$\theta$的策略$\pi_{\theta}$采样得到的轨迹的分布，也就是一系列$(s,a)$对概率的乘积，表示从$s_0$开始，经过一系列的动作$a_0,a_1,…,a_n$游戏结束的概率，即

$$P(\tau) = \prod_{t=0}^{n}P_{\theta}(a_t|s_t)$$

假设采样次数足够多，那么我们可以认为$\theta$的策略$\pi_\theta$为从$s_0$出发到游戏结束的轨迹的分布($\tau\sim\pi_\theta$)。期望回报也可以写出轨迹回报的积分形式

$$E_{\tau\sim \pi_{\theta}}[R(\tau)] = \int P_{\theta}(\tau)R(\tau)d\tau$$

到这里，整个训练的目标就十分清晰了，我们的目标是最大化期望回报，即

$$\theta^* = \arg\max_{\theta}E_{\tau\sim P_{\theta}(\tau)}[R(\tau)]$$

原理上理解了，而这个期望可以看作是一个关于$\theta$的函数。找到让这个函数最大的$\theta$，就是我们的目标。如何实现这一目标呢，（你想的对，牛顿法）我们可以用梯度上升法来实现这一目标。同时我们可以注意到，期望回报的两项中，$P_{\theta}(\tau)$是关于$\theta$的函数，而$R(\tau)$的计算是不依赖于$\theta$的，所以我们可以将期望回报的梯度进一步展开并化简

$$\begin{aligned} \nabla_{\theta}E_{\tau\sim P(\tau)}[R(\tau)] &= \nabla_{\theta}\sum_{\tau}P_{\theta}(\tau)R(\tau)\\ &= \sum_{\tau}\nabla_{\theta}P_{\theta}(\tau)R(\tau)\\ &= \sum_{\tau}R(\tau)\nabla_{\theta}P_{\theta}(\tau)\\ &= \sum_{\tau}R(\tau)\nabla_{\theta}\prod_{t=0}^{n}P_{\theta}(a_t|s_t)\\ &\propto \sum_{\tau}R(\tau)\nabla_{\theta}\sum_{t=0}^{n}\log P_{\theta}(a_t|s_t) \end{aligned}$$

在展开的最后一步，我把对$\tau$中每次状态转移的概率的求导展开成了对它的对数求导，这样一方面避免了累乘导致的数值消失，另一方面我们也可以对么一个$\tau$中的每一个$(s,a)$对的logit求导，这样就可以对每一个$(s,a)$对的概率进行更新。

根据该梯度公式，我们可以按照如下步骤进行训练：

1. 初始化$\theta$
2. 采样一系列的轨迹$\pi_{\theta}$
3. 遍历这些轨迹，对每条轨迹$\tau \in \pi_{\theta}$，计算$R(\tau)$
4. 对$\tau$中对时间步$t = 0,1,...,n$，做如下更新
   1. 计算$\nabla_{\theta}\log P_{\theta}(a_t|s_t)$
   2. 更新$\theta = \theta + \alpha R(\tau)\nabla_{\theta}\log P_{\theta}(a_t|s_t)$
5. 重复2步骤直至收敛

这就是Policy Gradient的训练过程，这个过程的核心是计算期望回报的梯度，然后根据梯度更新参数$\theta$。梯度计算中，只有每一个$(s,a)$对的概率是关于$\theta$的函数，而回报是不依赖于$\theta$的，最优化的迭代方向就是对于$R(\tau)$比较大的轨迹$\tau$，增大这个轨迹的概率，对于$R(\tau)$比较小的轨迹$\tau$，减小这个轨迹的概率。

RLHF: Reinforcement Learning with Human Feedback

以下内容系个人理解，可能有误，欢迎指正

观察刚刚提到的Policy Gradient的训练过程，我们可以发现，这个过程是一个无监督的过程，它只需要环境的反馈（即对每一个轨迹的评分），而不需要一个标注好的数据集。

大语言模型的训练过程剧场常见的梯度下降，每次蒙上句子的下一个token，根据上下文生成每一个位置对应的下一个token的概率分布，使用交叉熵损失函数计算这个概率分布与真实token的差距，然后更新参数。

大语言模型补全句子的过程，也可以理解为不断与环境交互的过程，$s_t$为t时刻的上下文，$a_t$为对$s_t$采取的token，取自$a_t = \max_{a}\pi_\theta(a|s_t)$，其中$\pi_\theta(s_t)$为模型预测的所有action的一个概率分布，也就是每一个token的概率，$\tau$就是整个生成完成的句子。

因为它的训练数据多是一些语料，比如新闻报道，维基百科，而并不是对话，受到这一数据集分布特点的影响，它补全句子倾向于让句子更加像训练数据集的概率分布，而不是对话的文本。这一点并不能满足AI assistant的需求，因为你没法和这样的补全句子的模型进行对话。因此我们需要增强这个模型的对话能力，即让他回复的句子更加符合对话的语境。同时我们也希望它的价值取向更倾向于人类对话场景的价值取向，比如礼貌，逻辑性等。那如何提高它采用出符合对话语境的句子$\tau$的概率呢？

SFT: Supervised Fine-Tuning

很容易想到，我们可以收集一个对话数据集，然后让这个模型在该数据集上进一步梯度下降，使得它的输出更加符合对话的语境。这个过程就是SFT，即在一个标注好的对话数据集上进行梯度下降，使得模型的输出更加符合对话的语境。

但是想象这么一个情况：

你希望它在补全“This is”的时候，说的话更像“This is a xxx”而不是“This is gonna xxx”，那标注数据中就可以让前者类型的语句更多，后者类型的语句更少。比如你的数据集里有“This is an apple”，但是没有“This is a banana”，可以预见的是，生成“This is an apple”的概率变大了，但是“This is a banana”的概率不一定会变大，甚至可能会变小。因为在计算$P_\theta(This \quad is\quad a)$的时候，我们假设它有三个选择（book, apple, banana），label是(0, 1, 0)，那么向损失函数（交叉熵）小的方向调整$\theta$就会更倾向于让它生成apple，而不是banana。但是其实我们更希望要的是(0.33, 0.33, 0.33)，因为三个选择都是合理的，而不是让它生成apple的概率更大。

这与我们的目的有所出入，我们希望的是让它生成的句子更符合你的需要，即让他补全this is的时候更倾向于表达这是一个什么东西（is sth），而不是表达将会发生什么（gonna happen）。而这样训练并不能达到这一效果，只是让它生成的句子更符合微调数据的分布。

HF: Human Feedback

为了实现这一目的，就需要量化什么样的句子是“你想要的句子”，也就是对每个句子你得去评价它是不是你想要的。而这对每个句子的评价其实就是所谓的人类反馈（Human Feedback）。当然，不能够是人去盯着对每个句子都打分，所以要搞一个方法来学习人的偏好，模拟人打分，即对Human Preference的建模。

这里，openai提出的方案是使用标注好的语句评分数据集来有监督地训练一个打分模型$R_\phi$，他对任何句子$\tau$都可以给出一个分数$R_\phi(\tau)$，这个分数表示这个句子符合你的期望的程度。那既然能够对每一个句子打分，那剩下的只需要让得分高的policy的概率变大，得分低的policy的概率变小就行了。这下就回到了我们上面提到的Policy Gradient的训练过程，使用这个打分模型$\phi$对预训练语言模型$\theta$做强化学习：

$$\begin{aligned} \arg\max_{\theta}E_{\tau\sim P_{\theta}(\tau)}[R_\phi(\tau)] &= \arg\max_{\theta}\sum_{\tau \in \pi_\theta}P_{\theta}(\tau)R_\phi(\tau)\\ \end{aligned}$$

通过最大化句子reward和句子的概率的乘积，我们就可以实现让打分高的句子的概率变大，打分低的句子的概率变小的目的。不同的地方仅仅在于这个$R_\phi(\tau)$是人类的偏好模型给出的，而不是环境的奖励。

当然RLHF还要更多的工作细节，包括了使用PPO（Proximal Policy Optimization）算法来提高训练的稳定性，以及使用GPT-3作为预训练模型等等。但是核心思想就是这样，通过人类的反馈来指导模型的训练，使得模型的输出更加符合人类的期望。

Why RL?

解释了RLHF的微调过程，不仅还是想问，即然有对每个句子的打分，为什么不直接用监督学习呢？这里我个人猜测核心原因在于：

1. 首先这个东西可以动态的调整模型。在使用ChatGPT的过程中常常会出现，它提供两个句子，你选一个符合你的偏好的然后继续聊天，这一次过程甚至可以被用于对模型微调（当然openai不可能这么直接用来微调，比较用户也不一定好好选）
2. 训练这个打分模型$R_\phi$，可以捕获到token embedding之间的相似性，比如数据集里给“This is an apple”打了高分，那么由于apple和banana之间比较相近（embedding空间上），在训练好的$R_\phi$上，给“This is a banana”也会打相对高的分数，通过这个评分模型来强化学习训练$\theta$可以使得$\theta$更好的学习到人类的偏好，生成更加符合人类偏好的句子，而不是生成更符合微调数据集分布的句子。

总结

这篇文章主要是记录了我对Policy Gradient的理解，以及对RLHF的一些思考。从传统的TQL（Tabular Q-Learning）介绍到DQL（Deep Q-Learning），从目的出发理解DQL存在的意义。然后介绍了Policy Gradient是参数化策略$\pi_\theta$以$s_0$为起点采样得到的轨迹的期望回报的梯度，并进一步对梯度进行了展开和化简，从而解释了迭代更新策略参数的一般化方法。最后介绍了RLHF的训练原理，以及我个人对为什么要用RLHF而不是直接用SFT的见解。